Dividing a square piece of origami into 17 parts
Forum rules
READ: The Origami Forum Rules & Regulations
READ: The Origami Forum Rules & Regulations
Dividing a square piece of origami into 17 parts
What is the best way to divide a square piece of origami paper into 17 parts?
Todd
Todd
- Brimstone
- Buddha
- Posts: 1729
- Joined: November 23rd, 2004, 3:59 am
- Location: Colombia, South America
- Contact:
Re: Dividing a square piece of origami into 17 parts
Divide each side into 18 ths and cut off one strip on two edges.
Dividing into 18ths is done by dividing into 3rds, then each 3rd into 3rds again and then dividing those 9ths in half.
Dividing into 18ths is done by dividing into 3rds, then each 3rd into 3rds again and then dividing those 9ths in half.
Re: Dividing a square piece of origami into 17 parts
Crossing diagonals! Precrease the top and right edges into fourths, and make a crease from the bottom left corner to the first fourth up the right side.
In the same way, make a crease from the bottom right corner to the fourth on the top closest to the right side.
The intersection of these diagonals will be (16,4).
In the same way, make a crease from the bottom right corner to the fourth on the top closest to the right side.
The intersection of these diagonals will be (16,4).
- Brimstone
- Buddha
- Posts: 1729
- Joined: November 23rd, 2004, 3:59 am
- Location: Colombia, South America
- Contact:
Re: Dividing a square piece of origami into 17 parts
Tankoda, could you please elaborate on your answer? I did not understand what you meant, what would be the use of (16,4)?
Re: Dividing a square piece of origami into 17 parts
I'm not sure if that is what Tankoda ment, but it should work as well:
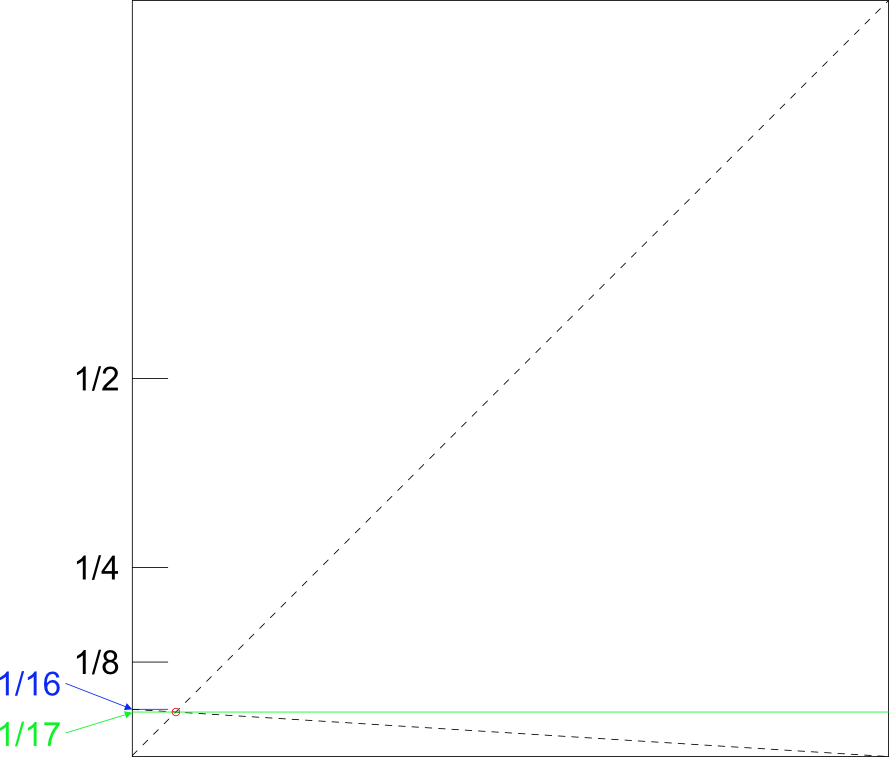
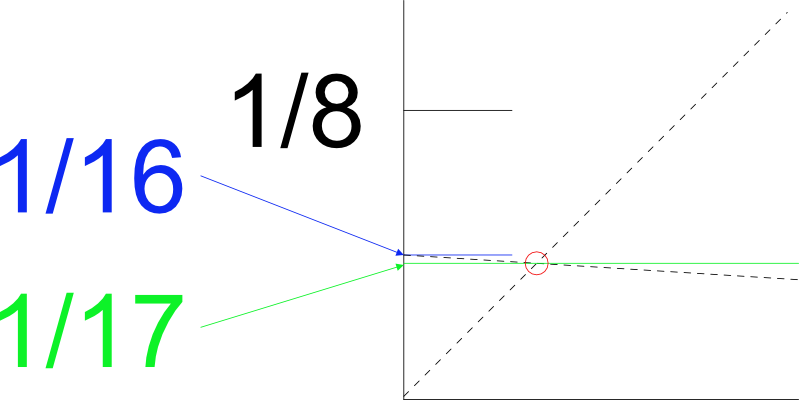
The left bottom corner zoomed in:
By the way, this works for other odd divisons as well. E.g to go from 1/4 -> 1/5 or from 1/8 -> 1/9...

The left bottom corner zoomed in:

By the way, this works for other odd divisons as well. E.g to go from 1/4 -> 1/5 or from 1/8 -> 1/9...
splunge.de - Origami, Papercraft, Scale models, Photography
Re: Dividing a square piece of origami into 17 parts
WOW... I had NO idea about this, and I like it a lot more than Brimstone's solution of cutting the paper after folding
Thank you Tankoda and Splunge!
.
My awesome website: https://www.neorigami.com
and Instagram account: https://instagram.com/NeorigamiCom
My awesome website: https://www.neorigami.com
and Instagram account: https://instagram.com/NeorigamiCom
-
Baltorigamist
- Moderator
- Posts: 2376
- Joined: December 25th, 2011, 7:15 pm
- Location: Inside my twisted mind....
Re: Dividing a square piece of origami into 17 parts
I second Tankoda's method.
Splunge's method would work in theory, but it's really difficult in practice. A diagonal of rectangle with anything more than about a 6:1 aspect ratio is really tricky to fold cleanly at the corner.
Gerardo, it works for irrational divisions as well. You can theoretically use that method for any real-number ratio you want; the only limit is the difficulty of constructing the numbers.
Splunge's method would work in theory, but it's really difficult in practice. A diagonal of rectangle with anything more than about a 6:1 aspect ratio is really tricky to fold cleanly at the corner.
Gerardo, it works for irrational divisions as well. You can theoretically use that method for any real-number ratio you want; the only limit is the difficulty of constructing the numbers.
Re: Dividing a square piece of origami into 17 parts
instead of using a crease to make the reference mark, use a ruler and a pencil. you will be happier in the long run.
Re: Dividing a square piece of origami into 17 parts
Baltorigamist is right that the method given by Splurge is hard in practice.
Also, Bethnor is right that a ruler and a pencil is more practical.
However, there is another method that uses a pencil but doesn’t need a ruler nor any calculation. It uses a second sheet of paper that has equally space lines ruled on it (usually for writing.) Method H of https://foldworks.net/wp-content/upload ... Thirds.pdf shows the method applied to thirds.

For 17ths, you would count 17 equal spaces. If the paper is large enough, you could use other multiples of 17 e.g. 34 or 68: the aim is to make the angle between the ruled lines and the raw edge of the square close to 90 degrees. This reduces the uncertainty of deciding where the ruled lines meet the raw edge.
For a pure origami method without lined paper, you could crease the second sheet into 32nds, say.
Here are some sources of origami divisions:
• HATORI Koshiro https://web.archive.org/web/20200217212 ... dex-e.html
• British Origami Society Booklet 6, Geometric Division, Mick Guy
• PAPER FOLDING FRACTIONS: Does this work? Malcolm Swan https://www.atm.org.uk/write/MediaUploa ... -03-03.pdf
• The mathematics behind the folds. Part 4. Dividing lengths into equal parts https://www.foldworks.net/home/articles ... qual-parts
Also, Bethnor is right that a ruler and a pencil is more practical.
However, there is another method that uses a pencil but doesn’t need a ruler nor any calculation. It uses a second sheet of paper that has equally space lines ruled on it (usually for writing.) Method H of https://foldworks.net/wp-content/upload ... Thirds.pdf shows the method applied to thirds.

For 17ths, you would count 17 equal spaces. If the paper is large enough, you could use other multiples of 17 e.g. 34 or 68: the aim is to make the angle between the ruled lines and the raw edge of the square close to 90 degrees. This reduces the uncertainty of deciding where the ruled lines meet the raw edge.
For a pure origami method without lined paper, you could crease the second sheet into 32nds, say.
Here are some sources of origami divisions:
• HATORI Koshiro https://web.archive.org/web/20200217212 ... dex-e.html
• British Origami Society Booklet 6, Geometric Division, Mick Guy
• PAPER FOLDING FRACTIONS: Does this work? Malcolm Swan https://www.atm.org.uk/write/MediaUploa ... -03-03.pdf
• The mathematics behind the folds. Part 4. Dividing lengths into equal parts https://www.foldworks.net/home/articles ... qual-parts
Re: Dividing a square piece of origami into 17 parts
I just found an APPROXIMATE method. I usually favor EXACT solutions like the ones presented above but this one is so simple, I have to mention it.
Just fold a diagonal and a bisector (1), like half a kite base. Then fold along the second diagonal (2). The mark you get on the edge of the paper is almost at 12/17:
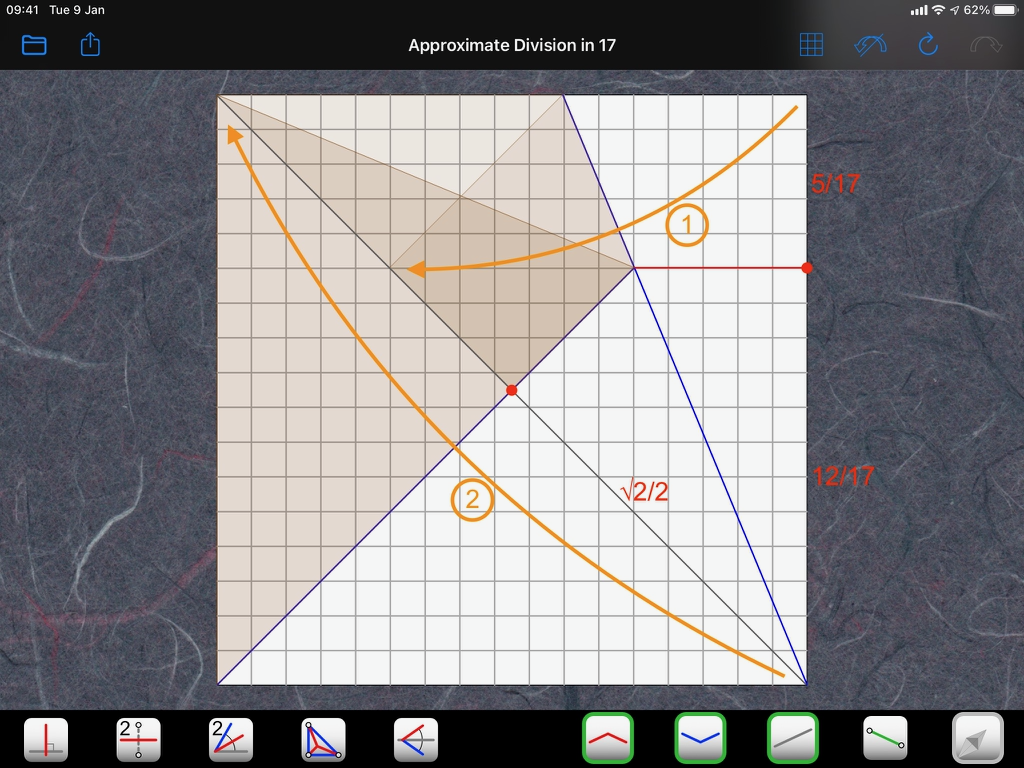
This is simply because 12/17 = 0.706, which is very close to half the square root of two (0.707).
It doesn't have the elegance of Tankoda's method but if you just want to get things done quickly, this may be your ticket.
Just fold a diagonal and a bisector (1), like half a kite base. Then fold along the second diagonal (2). The mark you get on the edge of the paper is almost at 12/17:

This is simply because 12/17 = 0.706, which is very close to half the square root of two (0.707).
It doesn't have the elegance of Tankoda's method but if you just want to get things done quickly, this may be your ticket.