Truncated Icosahedron
Forum rules
READ: The Origami Forum Rules & Regulations
READ: The Origami Forum Rules & Regulations
- RamblerMann66
- Newbie
- Posts: 26
- Joined: April 13th, 2006, 4:25 am
- Location: Berwyn, Illinois, USA
Truncated Icosahedron
is it possible to make this model...[http://picasaweb.google.com/lh/photo/I0 ... zHx-QeN1vA]...with only 3 colors and no two adjacent units are the same color? I'm too lazy to try and figure it out on my own, so a picture showing the pattern would be great
- Sara
- Senior Member
- Posts: 285
- Joined: January 25th, 2008, 9:18 am
- Location: Munich, Germany
- Contact:
Check http://books.google.com/books?id=_Nw4Hg ... q=&f=false
It includes a description and an image of the graph that you need to colour.
The basic idea is: first draw a graph, then find a Hamiltonian circuit in it (travel to all vertices without visiting any of the edges more than once, start and end in the same vertex). Next colour the Hamiltonian circle by alternating between two colours. Then determine the colours of the remaining edges. This is where you get to start using your third colour.
While this is not a complete solution, it is a very good starting point. I'm not sure how hard it is to manually find a Hamiltonian circuit, but you can read up on some theory / good algorithms. Maybe someone has posted a solution somewhere online, too.
-- Sara
It includes a description and an image of the graph that you need to colour.
The basic idea is: first draw a graph, then find a Hamiltonian circuit in it (travel to all vertices without visiting any of the edges more than once, start and end in the same vertex). Next colour the Hamiltonian circle by alternating between two colours. Then determine the colours of the remaining edges. This is where you get to start using your third colour.
While this is not a complete solution, it is a very good starting point. I'm not sure how hard it is to manually find a Hamiltonian circuit, but you can read up on some theory / good algorithms. Maybe someone has posted a solution somewhere online, too.
-- Sara
Last edited by Sara on September 23rd, 2009, 11:22 am, edited 1 time in total.
Yes, it's possible!
But it's very difficult to do with 90 edges because it's an NP-complete problem.
If you PM to me your e-mail address I'll send you a colored graph
But it's very difficult to do with 90 edges because it's an NP-complete problem.
If you PM to me your e-mail address I'll send you a colored graph
"There's a fold in everything..."
www.flickr.com/photos/mancinerie
www.flickr.com/photos/mancinerie
- Sara
- Senior Member
- Posts: 285
- Joined: January 25th, 2008, 9:18 am
- Location: Munich, Germany
- Contact:
I just did a search for a Hamiltonian circuit, and found this video:
http://www.youtube.com/watch?v=eIjcTZGTqQ8
Looks like the remaining edges (the ones not on the Hamiltonian circuit) will all be in the third colour.
This should solve the problem (and is more readily available than an image sent privately). I hope others will profit from it.
-- Sara
http://www.youtube.com/watch?v=eIjcTZGTqQ8
Looks like the remaining edges (the ones not on the Hamiltonian circuit) will all be in the third colour.
This should solve the problem (and is more readily available than an image sent privately). I hope others will profit from it.
-- Sara
The problem is not so simple as it seems (http://en.wikipedia.org/wiki/NP-complete_problem).Sara wrote: This should solve the problem (and is more readily available than an image sent privately). I hope others will profit from it.
You have to know at least the fundamentals of graph theory.
Anyway, if someone else is interested this is the graph (of course there are other solutions):
[img]http://img16.imageshack.us/img16/6301/bucky90.jpg[/img]
"There's a fold in everything..."
www.flickr.com/photos/mancinerie
www.flickr.com/photos/mancinerie
- Sara
- Senior Member
- Posts: 285
- Joined: January 25th, 2008, 9:18 am
- Location: Munich, Germany
- Contact:
Thanks for posting that image. I noticed that your colouring doesn't actually imply a Hamiltonian circuit, so I decided to give it a go. Below you'll see an image of an alternate colouring.
[fi-ori has circuits of length 6, 10, 10, 34. Check for example red and blue as the colours that imply the circuits.]
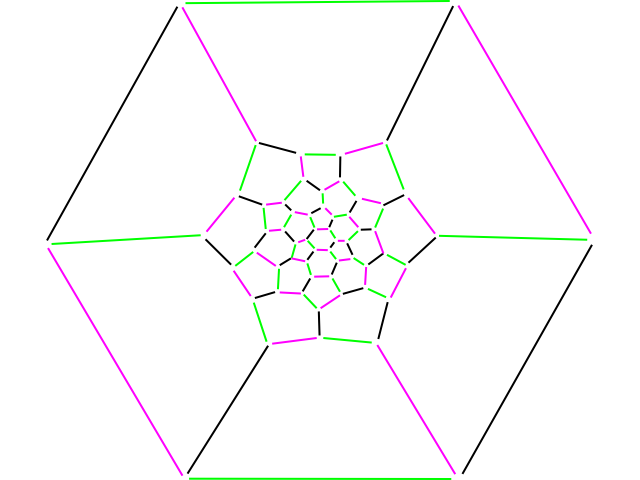
The interesting thing about this colouring is that every pentagon and hexagon has at least one module of each colour. It will give you a second option apart from the one fi-ori suggested. It'd be nice to see a picture of two truncated icosahedrons, each using a different colouring scheme. Anyone up for it?
By the way, I found it quite hard to extract the Hamiltonian circuit from the video, so I searched for one myself. So it might be a different one than the one that's shown in the video I linked to above. Not sure.
More: http://www.happyfolding.com/gallery-tru ... _colouring
[fi-ori has circuits of length 6, 10, 10, 34. Check for example red and blue as the colours that imply the circuits.]

The interesting thing about this colouring is that every pentagon and hexagon has at least one module of each colour. It will give you a second option apart from the one fi-ori suggested. It'd be nice to see a picture of two truncated icosahedrons, each using a different colouring scheme. Anyone up for it?
By the way, I found it quite hard to extract the Hamiltonian circuit from the video, so I searched for one myself. So it might be a different one than the one that's shown in the video I linked to above. Not sure.
More: http://www.happyfolding.com/gallery-tru ... _colouring
- RamblerMann66
- Newbie
- Posts: 26
- Joined: April 13th, 2006, 4:25 am
- Location: Berwyn, Illinois, USA
Nice coloration Sara! I'll give it a try!
This is an example of my 3-coloration of a truncated icosahedron made with PHiZZ units.
The colors are different from the graph but the pattern is the same

This is the same 3-coloration of another truncated icosahedron

This is an example of my 3-coloration of a truncated icosahedron made with PHiZZ units.
The colors are different from the graph but the pattern is the same

This is the same 3-coloration of another truncated icosahedron

"There's a fold in everything..."
www.flickr.com/photos/mancinerie
www.flickr.com/photos/mancinerie
- childofsai
- Junior Member
- Posts: 56
- Joined: September 11th, 2004, 11:02 pm
- Location: North London
- Contact:
- childofsai
- Junior Member
- Posts: 56
- Joined: September 11th, 2004, 11:02 pm
- Location: North London
- Contact:
- RamblerMann66
- Newbie
- Posts: 26
- Joined: April 13th, 2006, 4:25 am
- Location: Berwyn, Illinois, USA
here it is... http://www.facebook.com/photo.php?pid=1 ... 1435370357
Nicely done! 
What kind of unit you used?
Here I used Tom Hull's Bouncy units:

instead of pentagon and hexagons there are five- and six-pointed stars
What kind of unit you used?
Here I used Tom Hull's Bouncy units:

instead of pentagon and hexagons there are five- and six-pointed stars
"There's a fold in everything..."
www.flickr.com/photos/mancinerie
www.flickr.com/photos/mancinerie
- RamblerMann66
- Newbie
- Posts: 26
- Joined: April 13th, 2006, 4:25 am
- Location: Berwyn, Illinois, USA

