 For Tankoda (Take 2) by DirgeOfDreams, on Flickr
For Tankoda (Take 2) by DirgeOfDreams, on FlickrReference Help
Forum rules
READ: The Origami Forum Rules & Regulations
READ: The Origami Forum Rules & Regulations
-
Baltorigamist
- Moderator
- Posts: 2376
- Joined: December 25th, 2011, 7:15 pm
- Location: Inside my twisted mind....
Re: Reference Help
It's possible one of us miscalculated. Regardless, I figured it out with the image you sent me.
 For Tankoda (Take 2) by DirgeOfDreams, on Flickr
For Tankoda (Take 2) by DirgeOfDreams, on Flickr
 For Tankoda (Take 2) by DirgeOfDreams, on Flickr
For Tankoda (Take 2) by DirgeOfDreams, on FlickrReference point location help
Hello,
I am designing a model and this picture is the fundamental structure of the crease pattern. I would like some help to locate reference points to be able to fold this pattern from a square of any given size. And if it's not too much, I'd also like a mathematical explanation as to how to do this for my own future benefit. Thanks

I am designing a model and this picture is the fundamental structure of the crease pattern. I would like some help to locate reference points to be able to fold this pattern from a square of any given size. And if it's not too much, I'd also like a mathematical explanation as to how to do this for my own future benefit. Thanks

Re: Reference point location help
Hello,
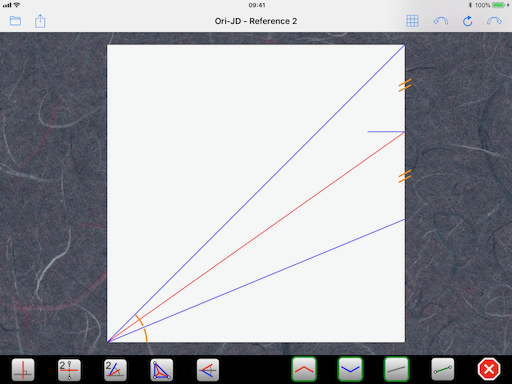
my estimation in Oripa resulted in the following:
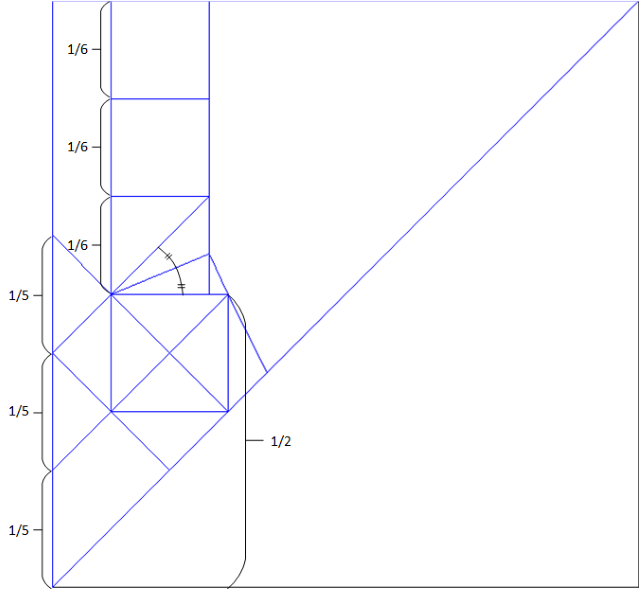
So it's based on a 30x30 grid
However, it doesn't exactly match your drawing, so I don't know if it's of any help for you:
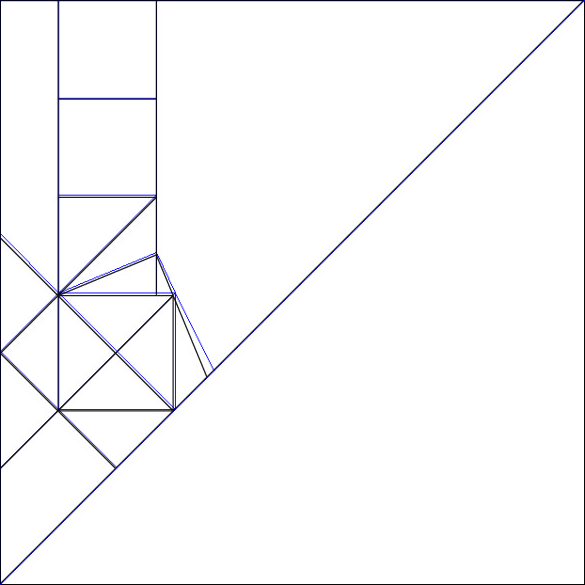
my estimation in Oripa resulted in the following:

So it's based on a 30x30 grid
However, it doesn't exactly match your drawing, so I don't know if it's of any help for you:

splunge.de - Origami, Papercraft, Scale models, Photography
Re: Reference point location help
I drew the CP in Adobe illustrator and tried determining what grid system it's using - but with no success. If I make the whole square 100 x 100mm, those three smaller squares are approximately 16.866 mm wide, while the slightly larger one is 19.76 mm wide.
I originally built the CP on a 10 x 10 grid, but made necessary structural changes. If you stack 10 squares from the bottom of the CP (aligning them perfectly with the existing edge creases), then you are left with 1.191 mm of space at the top...
I originally built the CP on a 10 x 10 grid, but made necessary structural changes. If you stack 10 squares from the bottom of the CP (aligning them perfectly with the existing edge creases), then you are left with 1.191 mm of space at the top...
-
Baltorigamist
- Moderator
- Posts: 2376
- Joined: December 25th, 2011, 7:15 pm
- Location: Inside my twisted mind....
Re: Reference point location help
Splunge, your estimation is off because it’s not based on a grid. It’s a complex irrational proportion that happens to almost lie on a grid.
Let me get back to you on this one. It will take some time to work out. In the meantime, draw lines from the corners through important points. They might hit the edges at easy-to-find points.
Also, I merged your topic with an existing one that covers reference points.
EDIT: as a starting point, each of the diagonals at the bottom left has length 2 (meaning the squares they form have side length 2sqrt2). Following that proportion, the squares stacked up to the top edge have side length 1+sqrt2. So the larger and smaller squares meet at 3+(3sqrt2) : 5sqrt2. (This is the top : bottom ratio.) As to why Splunge thought it was based on a grid, that line is 49.4% down from the top edge of the square.
I’ll try to work out a way to find that proportion tonight.
Let me get back to you on this one. It will take some time to work out. In the meantime, draw lines from the corners through important points. They might hit the edges at easy-to-find points.
Also, I merged your topic with an existing one that covers reference points.
EDIT: as a starting point, each of the diagonals at the bottom left has length 2 (meaning the squares they form have side length 2sqrt2). Following that proportion, the squares stacked up to the top edge have side length 1+sqrt2. So the larger and smaller squares meet at 3+(3sqrt2) : 5sqrt2. (This is the top : bottom ratio.) As to why Splunge thought it was based on a grid, that line is 49.4% down from the top edge of the square.
I’ll try to work out a way to find that proportion tonight.
-
Baltorigamist
- Moderator
- Posts: 2376
- Joined: December 25th, 2011, 7:15 pm
- Location: Inside my twisted mind....
Re: Reference Help
Forgive the double post, but I just decided to revisit this in case you’re still wondering how to find it. The ratio I came up with this time (top : bottom) is (9+(6sqrt2)) : (10+(5sqrt2)). I’ll have to crunch the numbers a little more to find the exact ratio, but as of now I don’t think it simplifies down.
Re: Reference Help
Sorry to come a little bit late to this; I was busy with other projects.
This is a perfect example of a problem you encounter with 22.5-degree designs, something you can indeed solve with some mathematics. It is actually the only type of design that is discussed in this thread, even though it is not explicitly named. I know the theory behind this was explained in several posts many years ago, but they are difficult to follow as the pictures have since disappeared. There is also a new tool that has appeared that can be very useful. So, I would like to give here a comprehensive explanation, step by step with fresh illustrations. It is a procedure adapted from an article by Satoshi Kamiya in Tanteidan Magazine (Folding Out 22.5 Degree and Relevant Angles, Tanteidan Magazine No. 115, p. 11 (2009)). It's going to be a bit lengthy, but I think it is worth it.
You start by assigning a unit length to some characteristic feature of your design from which it is easy to draw your pattern. Here, even though you say you started with a 10x10 grid and designed the crossed-out square in the lower part of the CP, it is actually easier to start with the three smaller squares at the top. So, let’s assign a unit length to these squares:
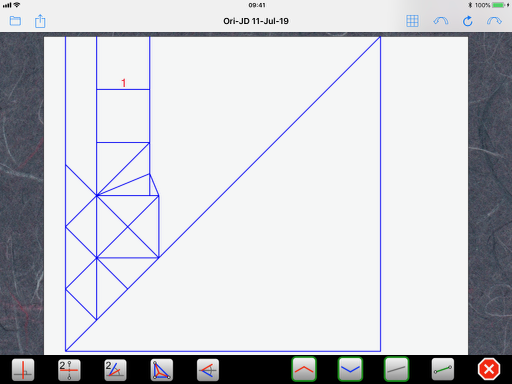
Next, we work out the size of the other features, step by step as we draw them. For this, we use three properties of triangles we encounter in 22.5-degree designs:
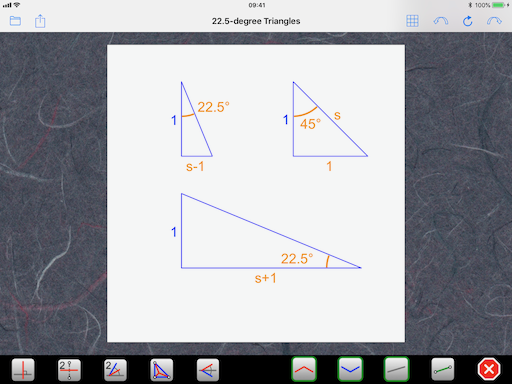
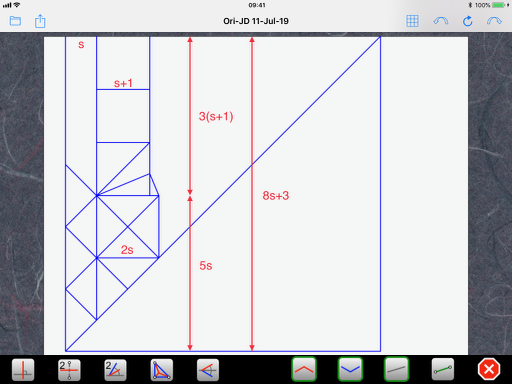
I use a personal notation to make it easier to read. “s” is actually the square root of 2, which is 1.4142… So, s times s, or s squared, or s^2, is 2. Using the above rules, we can deduce that the length of the diagonal of a small square is s and the height defined by the bisector (kite base) in the lowest of the three squares is s-1 (see rule #1 rotated 90 degrees):
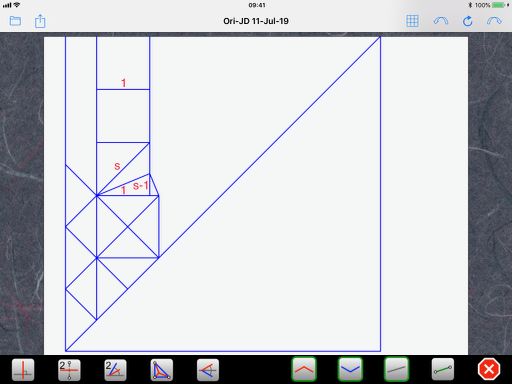
Next, we look at the tiny triangle that bridges the gap between the small square and the (slightly) bigger square. It too has the same shape as rule #1 (not rotated) but has a height of (s-1) instead of 1. So, all its dimensions are multiplied by (s-1) and we end up with (s-1) times (s-1) or (s-1)^2 for its base. To get the size of the bigger square, we simply add the size of the smaller square and we end up with 1+(s-1)^2:
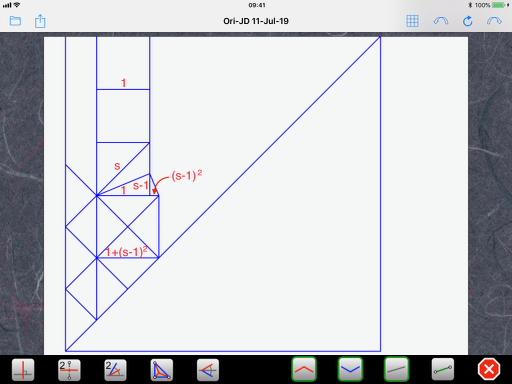
Here, we need a little bit of math in order to simplify things. You can skip to the following drawing if you are not interested in the details:
(s-1)^2 = (s-1)(s-1) = s^2-2s+1 = 2-2s+1 = 3-2s
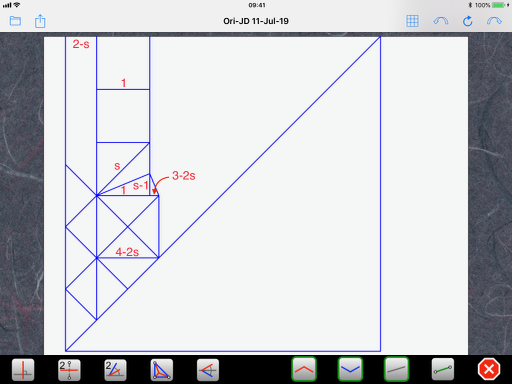
At the third equal sign, I used the property s^2 = 2. With this simplification, the size of the bigger square is now 4-2s, so the original grid is now assigned a size of 2-s:
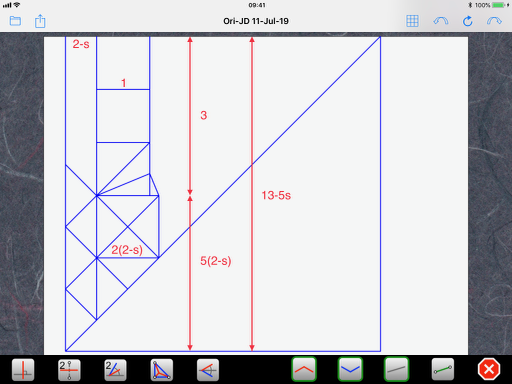
Summing up (literally), the three smaller squares at the top have a total height of 3 and the bottom part has five of the original grid size, or 5(2-s). The total height of the paper is 3+5(2-s) = 13-5s:
Now, we don’t like to have a negative sign in our paper size, so we have to use some more math to simplify this. This time, it is quite involved, so if you are not mathematically inclined, you either have to trust me or ask for some help. Here we go: we divide all dimensions by (2-s) and multiply them by s. So, we have the following transformations:
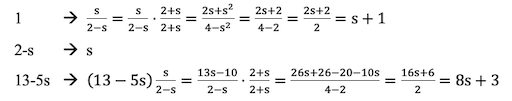
Did you follow me? In the first and last lines, I used the “multiply by the conjugate” technique to get rid of the denominator. See for example here for an easy explanation. If you are serious about all this, you will have to get used to this technique. Sorry, there is no free lunch here!
But here is the reward: we now have a cleaner picture with numbers that are easier to work with:
Most importantly, these are numbers that Satoshi Kamiya’s calculator can use. It is a calculator that he has developed for solving this kind of pattern. It is more useful in this case than Robert Lang’s Reference Finder. It is in Japanese, but it is easy to use if you have done the work above. You simply enter the total size of your paper in the two boxes at the top of the page and hit the button underneath. In this case, you enter “3” and “8” (because he wants the size to be entered as [] + []*s) and you get 19 possible solutions (with other sizes, you can get less or more or sometimes 0). He only shows the first one but there are “Previous” and “Next” buttons underneath to browse through all solutions.
Let’s look at the first solution. There are two drawings showing two specific folds we have to make (I have rotated them by 90 degrees):
Their intersection gives us a new reference specific to the dimension we gave. The calculator tells us this reference point lies at distance 3s from the left edge of the paper:
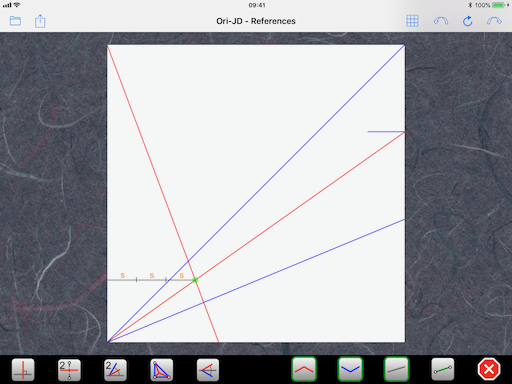
So, with a trisection, we get the vertical strip at distance s from the edge and we can start folding the CP:
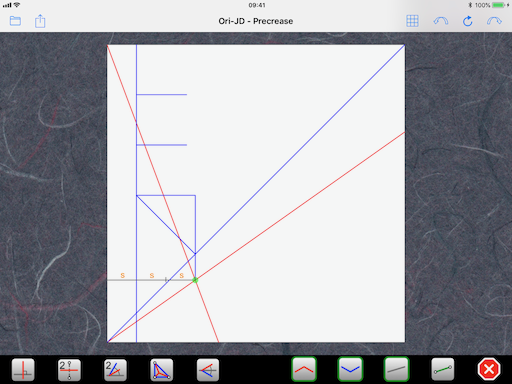
If you don’t like the trisection, you can select the next solution in Satoshi Kamiya’s calculator, which gives you 4s instead of 3s. Unfortunately, there is no solution that gives you directly 5s, so we always have to do some more folding to get to the three upper squares (which require a trisection anyway).
There you have it: not only a way to fold your design on any size paper but a procedure you can apply to any other design you make in the 22.5-degree system. Good luck!
This is a perfect example of a problem you encounter with 22.5-degree designs, something you can indeed solve with some mathematics. It is actually the only type of design that is discussed in this thread, even though it is not explicitly named. I know the theory behind this was explained in several posts many years ago, but they are difficult to follow as the pictures have since disappeared. There is also a new tool that has appeared that can be very useful. So, I would like to give here a comprehensive explanation, step by step with fresh illustrations. It is a procedure adapted from an article by Satoshi Kamiya in Tanteidan Magazine (Folding Out 22.5 Degree and Relevant Angles, Tanteidan Magazine No. 115, p. 11 (2009)). It's going to be a bit lengthy, but I think it is worth it.
You start by assigning a unit length to some characteristic feature of your design from which it is easy to draw your pattern. Here, even though you say you started with a 10x10 grid and designed the crossed-out square in the lower part of the CP, it is actually easier to start with the three smaller squares at the top. So, let’s assign a unit length to these squares:

Next, we work out the size of the other features, step by step as we draw them. For this, we use three properties of triangles we encounter in 22.5-degree designs:

I use a personal notation to make it easier to read. “s” is actually the square root of 2, which is 1.4142… So, s times s, or s squared, or s^2, is 2. Using the above rules, we can deduce that the length of the diagonal of a small square is s and the height defined by the bisector (kite base) in the lowest of the three squares is s-1 (see rule #1 rotated 90 degrees):

Next, we look at the tiny triangle that bridges the gap between the small square and the (slightly) bigger square. It too has the same shape as rule #1 (not rotated) but has a height of (s-1) instead of 1. So, all its dimensions are multiplied by (s-1) and we end up with (s-1) times (s-1) or (s-1)^2 for its base. To get the size of the bigger square, we simply add the size of the smaller square and we end up with 1+(s-1)^2:

Here, we need a little bit of math in order to simplify things. You can skip to the following drawing if you are not interested in the details:
(s-1)^2 = (s-1)(s-1) = s^2-2s+1 = 2-2s+1 = 3-2s
At the third equal sign, I used the property s^2 = 2. With this simplification, the size of the bigger square is now 4-2s, so the original grid is now assigned a size of 2-s:

Summing up (literally), the three smaller squares at the top have a total height of 3 and the bottom part has five of the original grid size, or 5(2-s). The total height of the paper is 3+5(2-s) = 13-5s:

Now, we don’t like to have a negative sign in our paper size, so we have to use some more math to simplify this. This time, it is quite involved, so if you are not mathematically inclined, you either have to trust me or ask for some help. Here we go: we divide all dimensions by (2-s) and multiply them by s. So, we have the following transformations:
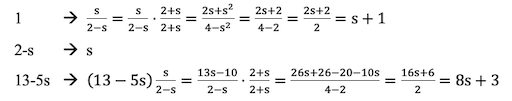
Did you follow me? In the first and last lines, I used the “multiply by the conjugate” technique to get rid of the denominator. See for example here for an easy explanation. If you are serious about all this, you will have to get used to this technique. Sorry, there is no free lunch here!
But here is the reward: we now have a cleaner picture with numbers that are easier to work with:

Most importantly, these are numbers that Satoshi Kamiya’s calculator can use. It is a calculator that he has developed for solving this kind of pattern. It is more useful in this case than Robert Lang’s Reference Finder. It is in Japanese, but it is easy to use if you have done the work above. You simply enter the total size of your paper in the two boxes at the top of the page and hit the button underneath. In this case, you enter “3” and “8” (because he wants the size to be entered as [] + []*s) and you get 19 possible solutions (with other sizes, you can get less or more or sometimes 0). He only shows the first one but there are “Previous” and “Next” buttons underneath to browse through all solutions.
Let’s look at the first solution. There are two drawings showing two specific folds we have to make (I have rotated them by 90 degrees):


Their intersection gives us a new reference specific to the dimension we gave. The calculator tells us this reference point lies at distance 3s from the left edge of the paper:

So, with a trisection, we get the vertical strip at distance s from the edge and we can start folding the CP:

If you don’t like the trisection, you can select the next solution in Satoshi Kamiya’s calculator, which gives you 4s instead of 3s. Unfortunately, there is no solution that gives you directly 5s, so we always have to do some more folding to get to the three upper squares (which require a trisection anyway).
There you have it: not only a way to fold your design on any size paper but a procedure you can apply to any other design you make in the 22.5-degree system. Good luck!
Re: Reference Help
P.S.:
You may be wondering why I don’t get the same result at Baltorigamist:
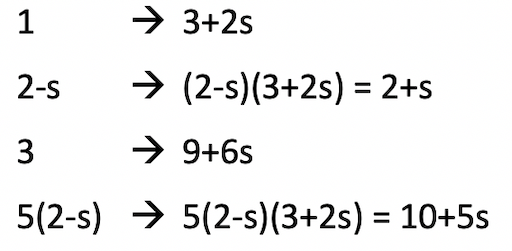
and thus:
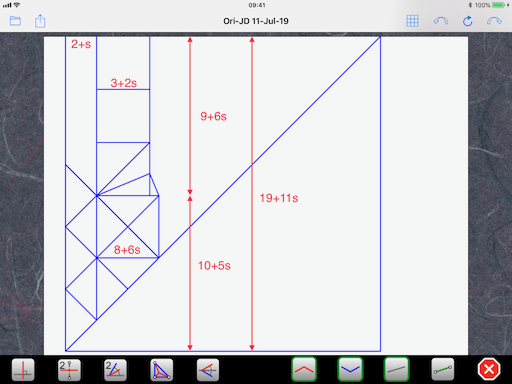
which is Baltorigamist’s solution. Now, if you enter this paper size (19+11s) in Satoshi Kamiya’s calculator, you get no less than 59 possibilities! You have to sift through them and hope to find one that helps you get the CP started.
In general, the smaller the numbers in the final paper size, the easier it is for the calculator to find a usable construction. Unfortunately, there is no algorithm that I know of that would allow you to find the smallest numbers. It is through trial and error that we find the best solution, if there is one. Sometimes, there is no good solution and the calculator cannot find you any way to build the reference you need (although it can be demonstrated that there is always a way).
In such cases, an approximate solution you can find with Robert Lang’s Reference Finder may save the day. Sometimes, an approximate solution can lead to a more accurate result on paper than a theoretically exact one. Origami is not all math... even though it is fun to solve a problem like this one!
You may be wondering why I don’t get the same result at Baltorigamist:
Actually, I do. It is just that I didn’t express it the same way. There is in fact an infinity of other expressions possible. If you start from my solution and, instead of multiplying everything by s/(2-s), you multiply by (3+2s), you get:Baltorigamist wrote:The ratio I came up with this time (top : bottom) is (9+(6sqrt2)) : (10+(5sqrt2)).
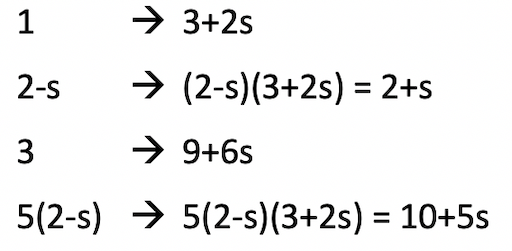
and thus:

which is Baltorigamist’s solution. Now, if you enter this paper size (19+11s) in Satoshi Kamiya’s calculator, you get no less than 59 possibilities! You have to sift through them and hope to find one that helps you get the CP started.
In general, the smaller the numbers in the final paper size, the easier it is for the calculator to find a usable construction. Unfortunately, there is no algorithm that I know of that would allow you to find the smallest numbers. It is through trial and error that we find the best solution, if there is one. Sometimes, there is no good solution and the calculator cannot find you any way to build the reference you need (although it can be demonstrated that there is always a way).
In such cases, an approximate solution you can find with Robert Lang’s Reference Finder may save the day. Sometimes, an approximate solution can lead to a more accurate result on paper than a theoretically exact one. Origami is not all math... even though it is fun to solve a problem like this one!
-
Baltorigamist
- Moderator
- Posts: 2376
- Joined: December 25th, 2011, 7:15 pm
- Location: Inside my twisted mind....
Re: Reference Help
Very interesting. It’s good to know that I at least got the right proportion (even if it was the second time around). 
I’d be very interested in learning more about how to find reference points (i.e., the methodology behind Satoshi’s calculator).
I’d be very interested in learning more about how to find reference points (i.e., the methodology behind Satoshi’s calculator).
Re: Reference Help
He essentially searches through a list of possibilities for each of the two folds, one from the lower left corner, the other from the lower right corner, and outputs the combinations that give the desired intersection point. It is not overly complicated but cleverly done. And the graphical output is really a plus.
Re: Reference Help
If you look at the source code of Kamiya's calculator page, you can get some information about it.Baltorigamist wrote:I’d be very interested in learning more about how to find reference points (i.e., the methodology behind Satoshi’s calculator).
Re: Reference Help
no all this talk of √2 nth powers does my brain in .They should just invent a scanner .like a barcode label scanner but for crease patterns instead .I imagine plenty would be lost of it 
 werent for calculators ..
werent for calculators ..
-
greencube07
- Senior Member
- Posts: 283
- Joined: August 9th, 2013, 3:21 am
Re: Reference Help

Can anyone help me fine the reference for this raito? I really need it for the new model but can't seem to find it..
thanks in advance guys.
;it's 2√2 : 0.5 : 2√2 : 1: 2√2
my flickr - http://www.flickr.com/photos/95668554@N06/
Re: Reference Help
There are ways to fold this but they are not easy.
A first reference is easy to find: writing "s" for √2, the entire ratio can be written (2s : 0.5 : 2s : 0.5 : 0.5 : 2s) or (2s : 0.5) : (2s : 0.5) : (0.5 : 2s). That is three times (2s : 0.5). So, the point after 0.5 is at 1/3 of the diagonal.
Then, within each third, you have to build the ratio (2s : 0.5) or (4s : 1). Entering that in Satoshi Kamiya's calculator, you get several solutions. Unfortunately, none of them is easy to apply to a square built on the third of a paper. Alternatively, you could divide first in the (4s : 1) ratio, then divide in three using the successive approximations method.
Good luck.
A first reference is easy to find: writing "s" for √2, the entire ratio can be written (2s : 0.5 : 2s : 0.5 : 0.5 : 2s) or (2s : 0.5) : (2s : 0.5) : (0.5 : 2s). That is three times (2s : 0.5). So, the point after 0.5 is at 1/3 of the diagonal.
Then, within each third, you have to build the ratio (2s : 0.5) or (4s : 1). Entering that in Satoshi Kamiya's calculator, you get several solutions. Unfortunately, none of them is easy to apply to a square built on the third of a paper. Alternatively, you could divide first in the (4s : 1) ratio, then divide in three using the successive approximations method.
Good luck.